好好玩

即对于k∈[1,t] 求(ax+by)^k

以下图片均来自于：

一

 

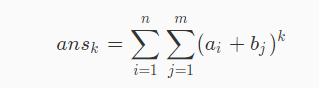
二项式展开：

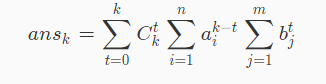
 设：

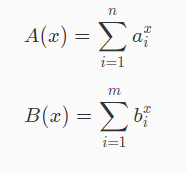
那么：

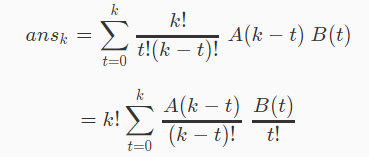
可以卷积了

二

求：

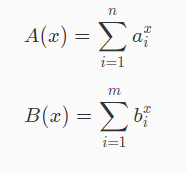
（PS：随机序列的0~k次方和，这是一个经典问题。）

我的思路：O(nk)暴力

神仙思路：求一个毫不沾边的东西，然后写两次，对应上系数。O(nlog^2n)

 

不妨考虑求A(x)：

先求一个看起来毫不沾边的东西：

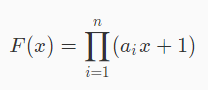
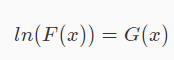
这个G成为了写两次的东西

解决问题的中轴和杠杆

 

利用

分治NTT+求Ln

现在已经写了一次

 

写第二次：

 

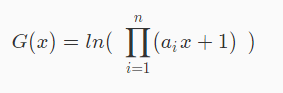
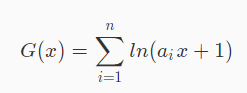
对于单独一项，采用Taylor展开，往多项式方向靠近

合起来：

交换顺序：

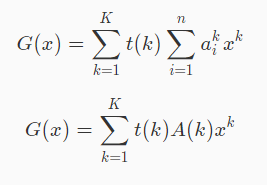
哇！

写第二次，

用Taylor展开+交换求和号

对应系数直接相等

 

神仙神仙~！~~~！！~！

 

Code

多项式全家桶

const int N=1e5+5;int n,m,K;int a[N],b[N];int A[N],B[N];int c[N];int jie[N],inv[N];il Poly divi(int l,int r){    if(l==r){        Poly g;g.resize(2);g[0]=1;g[1]=c[l];return g;    }    int mid=(l+r)>>1;    Poly L=divi(l,mid),R=divi(mid+1,r);    return L*R;}void wrk(int *a,int *A,int n){        for(reg i=1;i<=n;++i) c[i]=a[i];    Poly G=divi(1,n);    // G.out();    G.resize(K+4);    G=Ln(G);       G.resize(K+1);    // G.out();    for(reg k=1;k<=K;++k){        if((k+1)&1){            A[k]=mod-mul(G[k],k);        }else{            A[k]=mul(G[k],k);        }    }}int main(){    rd(n);rd(m);    for(reg i=1;i<=n;++i){        rd(a[i]);    }    for(reg i=1;i<=m;++i){        rd(b[i]);    }    rd(K);    wrk(a,A,n);    wrk(b,B,m);    A[0]=n;    B[0]=m;    // prt(A,0,K);    // prt(B,0,K);    Poly f,g;    f.resize(K+1);g.resize(K+1);    jie[0]=1;    for(reg i=1;i<=K;++i) jie[i]=(ll)jie[i-1]*i%mod;    inv[K]=qm(jie[K],mod-2);    for(reg i=K-1;i>=0;--i) inv[i]=mul(inv[i+1],i+1);    for(reg i=0;i<=K;++i){        f[i]=mul(A[i],inv[i]);        g[i]=mul(B[i],inv[i]);    }    f=f*g;    for(reg i=1;i<=K;++i){        ll ans=mul(jie[i],f[i]);        ans=mul(ans,qm(mul(n,m),mod-2));        printf("%lld\n",ans);    }    return 0;}